Java String、StringBuffer、StringBuilder(基于源码探索)
本文共 2510 字,大约阅读时间需要 8 分钟。
String、StringBuffer、StringBuilder
1、String
String是Java类对象,Java通过String来创建和操作字符串。
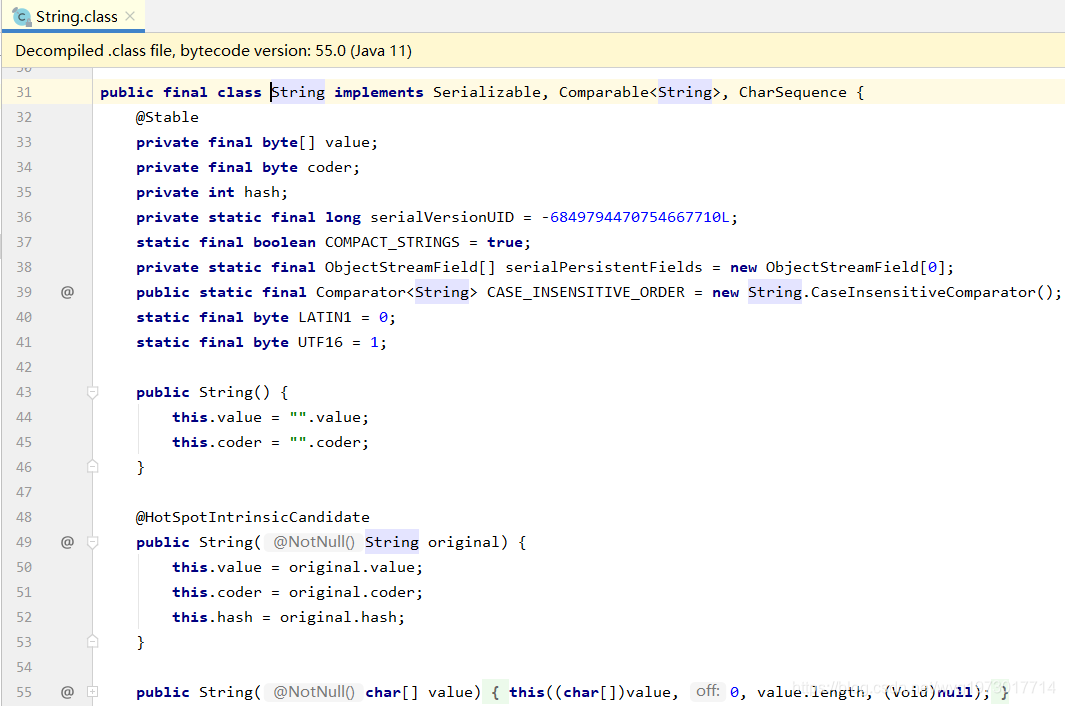
从源码中我们可以看出,String使用byte[]数组进行字符串的存储,且byte[]数组被final关键字修饰。我们知道当final修饰成员变量时,如果成员变量是基本数据类型的变量那么该变量一旦初始化以后就不可更改,源码中value数组是在构造方法中赋初值,因此String类对象一旦被创建就不可更改。
故String类对象是不可变的。
 在实际应用过程中,我们可以通过 + 号来连接两个字符串,然后输出一个新的字符串
在实际应用过程中,我们可以通过 + 号来连接两个字符串,然后输出一个新的字符串 public static void main(String[] args) { String a = "wyg and "; String b = "wind"; System.out.print(a + b);} 以上代码运行输出以下结果
 虽然String类对象不可变,但是我们可以通过加号(+)来进行拼接两个字符串,或者通过String提供的函数concat(String str),下面是其源码,我们可以发现concat方法直接返回了一个新的String类对象。
虽然String类对象不可变,但是我们可以通过加号(+)来进行拼接两个字符串,或者通过String提供的函数concat(String str),下面是其源码,我们可以发现concat方法直接返回了一个新的String类对象。 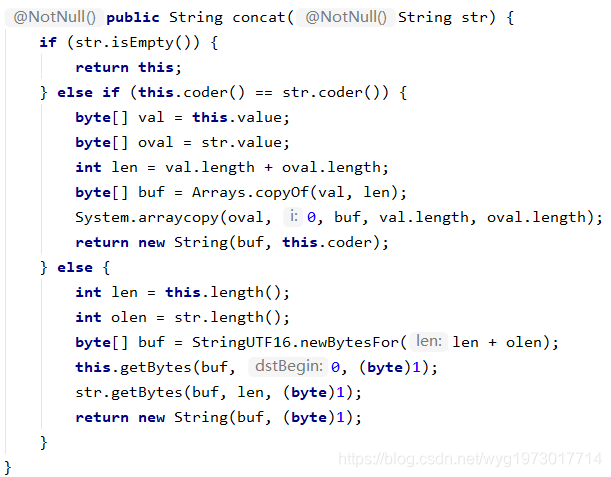 还有一种情况请看以下代码:
还有一种情况请看以下代码: public static void main(String[] args) { String a = "wyg and "; a = a + "wind"; System.out.print(a);} 代码输出结果为wyg and wind
这样看似String对象a被改变了,但是实际上并非如此,而是在在运行过程中JVM又创建了一个a对象,并把原a对象和新增字符串的值赋值给了这个新对象,然后原a对象就被JVM的GC(垃圾回收机制)给回收掉了。
Java中对String对象进行的操作实际上是一个不断创建新的对象并且将旧的对象回收的一个过程,所以执行速度很慢。
String类还有很多有用的方法,可以在具体使用中通过源码进行研究
2、StringBuffer
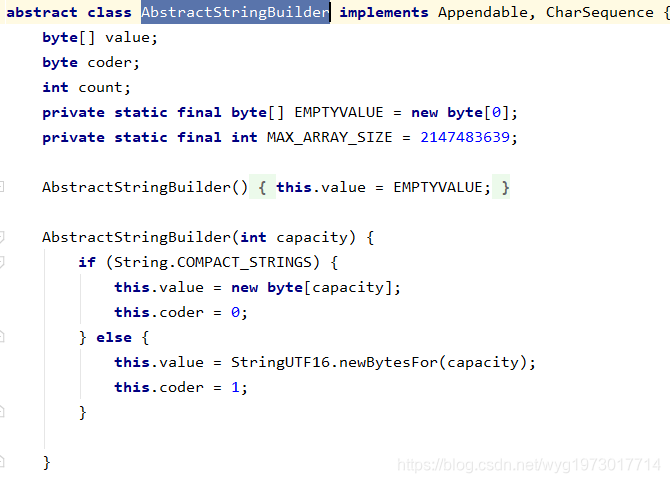
StringBuffer类继承自AbstractStringBuilder类
 AbstractStringBuilder类的成员变量value也是byte类型数组,但是未被final关键字修饰,因此我们可以知道该成员变量是可变的
AbstractStringBuilder类的成员变量value也是byte类型数组,但是未被final关键字修饰,因此我们可以知道该成员变量是可变的 故StringBuffer是可变字符串
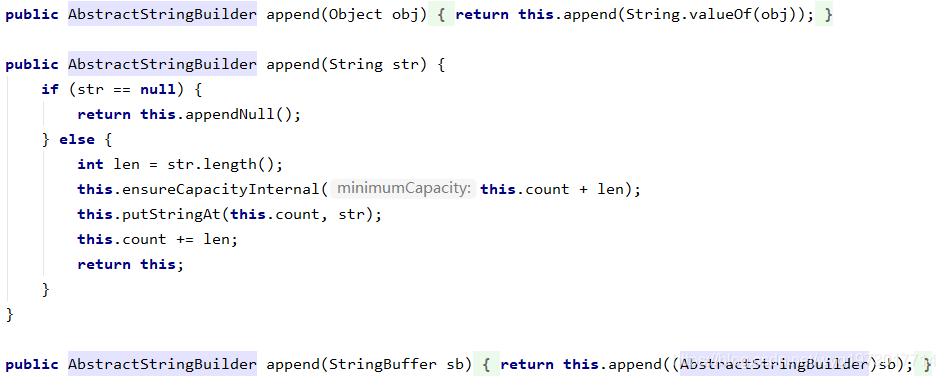
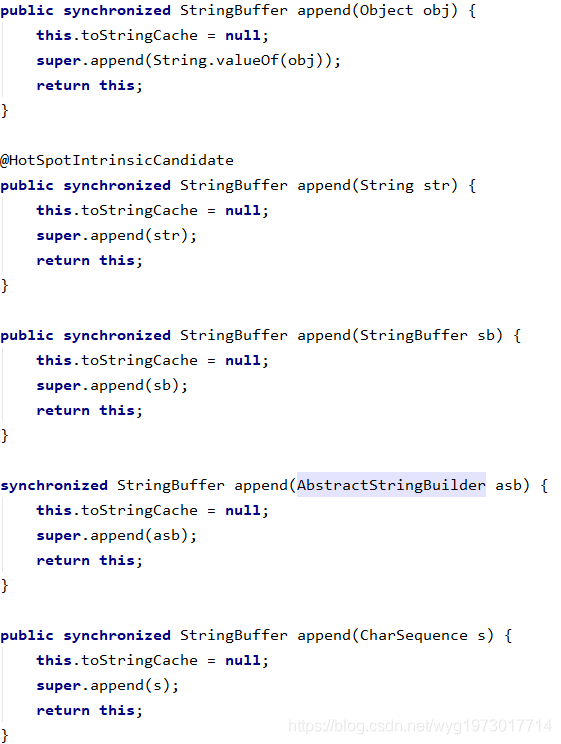 除了append函数以外还有replace、insert等函数来改变StringBuffer对象的值。具体可以参考源码
除了append函数以外还有replace、insert等函数来改变StringBuffer对象的值。具体可以参考源码 3、StringBuilder

其他具体方法的实现不再赘述。
4、StringBuffer与StringBuilder区别
(1)缓冲区
以下是StringBuffer的toString()方法:@HotSpotIntrinsicCandidate public synchronized String toString() { return this.toStringCache == null ? (this.toStringCache = this.isLatin1() ? StringLatin1.newString(this.value, 0, this.count) : StringUTF16.newString(this.value, 0, this.count)) : new String(this.toStringCache); } 从中我们可以看出StringBuffer每次获取 toString 都会直接使用缓存区的 toStringCache 值来构造一个字符串
再来看看StringBuilder的toString()方法:@HotSpotIntrinsicCandidate public String toString() { return this.isLatin1() ? StringLatin1.newString(this.value, 0, this.count) : StringUTF16.newString(this.value, 0, this.count); } 可知StringBuilder 每次都需要复制一次字符数组,再构造一个字符串。
StringBuffer的缓冲区是对其自身的一种优化,同时,他也是同步的方法,线程安全。 (2)性能 StringBuffer 是线程安全的,它的所有公开方法都是同步的,StringBuilder 是没有对方法加锁同步的,所以毫无疑问,StringBuilder 的性能要远大于StringBuffer。5、实际运用如何选择?
- StringBuffer 适用于用在多线程操作同一个 StringBuffer 的场景,如果是单线程场合 StringBuilder 更适合。
- 实际运行速度:StringBuilder > StringBuffer > String,StringBuilder 效率最高
- 操作少量的数据可以选择String
- 在单线程中操作大量数据可以选择StringBuilder
- 在多线程中操作大量数据可以选择StringBuffer
- https://www.zhihu.com/question/20101840 可以看看知乎上这个问题
转载地址:http://cteo.baihongyu.com/
你可能感兴趣的文章
Netty工作笔记0031---NIO零拷贝应用案例
查看>>
Netty工作笔记0032---零拷贝AIO内容梳理
查看>>
Netty工作笔记0033---Netty概述
查看>>
Netty工作笔记0034---Netty架构设计--线程模型
查看>>
Netty工作笔记0035---Reactor模式图剖析
查看>>
Netty工作笔记0036---单Reactor单线程模式
查看>>
Netty工作笔记0037---主从Reactor多线程
查看>>
Netty工作笔记0038---Netty模型--通俗版
查看>>
Netty工作笔记0039---Netty模型--详细版
查看>>
Netty工作笔记0040---Netty入门--服务端1
查看>>
Netty工作笔记0041---Netty入门--服务端2
查看>>
Netty工作笔记0042---Netty入门--编写客户端
查看>>
Netty工作笔记0043---单Reactor多线程模式
查看>>
Netty工作笔记0044---Netty案例源码分析
查看>>
Netty工作笔记0044---scheduledTaskQueue
查看>>
Netty工作笔记0045---Netty模型梳理
查看>>
Netty工作笔记0045---异步模型原理剖析
查看>>
Netty工作笔记0046---TaskQueue自定义任务
查看>>
Netty工作笔记0046---异步模型原理剖析
查看>>
Netty工作笔记0047---Http服务程序实例
查看>>